Talvolta è accaduto che importanti ritrovamenti archeologici siano stati frutto del caso. Un evento di questo genere è all'origine della nostra vicenda: durante i lavori eseguiti per il consolidamento della struttura di un palazzo di Matelica, in provincia di Macerata, fu rinvenuto, nel 1985, un globo di marmo. Uno di noi (Baldini) ebbe modo di esaminarlo con accuratezza e si rese conto della possibile importanza di questo oggetto, a tutt'oggi apparentemente unico.

Il globo, o sfera, fu riposto nel Museo Piersanti di Matelica per ulteriori esami. È balzato subito all'occhio che si doveva trattare di uno strumento per la misura del tempo, di una meridiana, in poche parole. Solo recentemente, però, ci è stato possibile effettuare un dettagliato studio delle funzioni di questo strumento: siamo ora in grado di spiegarne le caratteristiche. 

Abbiamo detto che l'oggetto è apparentemente unico: un suo parente stretto, ritrovato nel 1939 da Carl W. Blegen tra le rovine di Prosymna, si trova al Museo di Nafplion, in Grecia. I due globi, tuttavia, differiscono profondamente nei dettagli costruttivi e, molto probabilmente, nelle modalità d'uso. 

In questo articolo ci dedicheremo esclusivamente alla descrizione del globo di Matelica da un punto di vista tecnico: faremo cioè quello che farebbe un informatico del Quarantesimo secolo che si trovasse tra le mani un calcolatore dei giorni nostri. Molti aspetti archeologici, che sicuramente riserveranno interessanti sorprese, verranno completamente trascurati, sia per incompetenza degli autori che per ovvi limiti di spazio. L'oggetto in questione ha tuttavia un interesse cosi profondo per l'archeoastronomia da giustificare di sorvolare per il momento sugli aspetti propriamente storici.

La sfera di Matelica è di marmo. Essa misura circa 14,6 cm di raggio medio. Per la verità non è proprio sferica: l'emisfero inferiore è deformato da un profondo incavo, evidentemente destinato alla messa in posto dello strumento, e da una tacca aggiuntiva - probabilmente alloggiamento di qualche supporto di legno o bronzo - per evitare oscillazioni. Anche l'emisfero superiore non è perfettamente sferico (con scarti di qualche millimetro); questo può essere spiegato dalle difficoltà di costruzione, o dall'erosione cui la sfera è stata soggetta nel tempo.

Le incisioni presenti – tuttora ben leggibili - fanno tuttavia pensare che quest'ultimo processo non sia stato particolarmente distruttivo. Nella nostra descrizione ci limiteremo all'emisfero superiore, delimitato nel piano equatoriale da una linea incisa che chiameremo "orizzonte". Perpendicolarmente ad essa è incisa un'altra linea che chiameremo "meridiano".  Le due linee si vedono chiaramente nella foto qui a lato. Dividendo idealmente l'emisfero superiore con un piano perpendicolare all'equatore, otteniamo due quarti di sfera, uno dei quali presenta tre cerchi concentrici intersecati da un quarto arco di cerchio (foto 1); l'altro quarto è invece praticamente liscio, a parte una serie di 13 fori (foto 2), disposti in una figura a cuspide con il foro centrale esattamente al culmine e gli estremi sull'orizzonte, a 90 gradi dal meridiano.

Foto 1. La faccia anteriore della sfera contiene tre cerchi concentrici, intersecati da un arco di cerchio. Il centro dei cerchi giace sulla linea meridiana	Foto 2. Vista dall'alto la sfera presenta una serie di 13 fori, organizzati a forma di cuspide. Il foro centrale è alla sommità della sfera, mentre i due fori estremi, considerevolmente più grandi degli altri si trovano sull'"orizzonte"

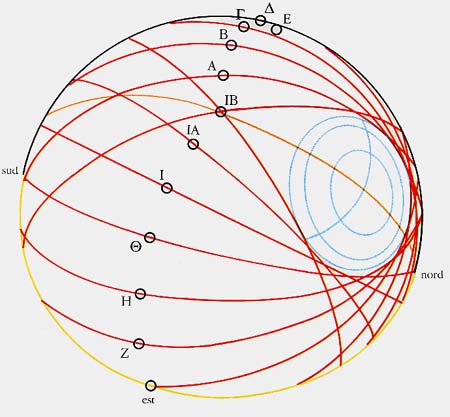
Chiameremo il quarto con i cerchi "faccia anteriore" e quello con i fori "faccia posteriore". I fori sono numerati, a partire dal primo a destra del culmine guardando la faccia anteriore, da alfa ad epsilon maiuscole (A, B, Γ, Δ, E); il sesto foro (a destra sull'orizzonte) è indicato con il simbolo digamma. Il primo foro a sinistra (sempre sull'orizzonte) è ancora indicato con un digamma, anche se speculare rispetto all'altro simbolo. Quindi la numerazione riprende da zeta a iota maiuscole (Z, H, Θ, I) per continuare con IA (iota-alfa) e per finire con il foro di colmo, contrassegnato con IB (iota-beta). 

Accanto ad alcuni di questi fori, che hanno dimensioni di circa 2 mm, vi sono dei minuscoli forellini, sul cui possibile significato torneremo più avanti. I due fori sull'orizzonte sono considerevolmente più grandi degli altri: in quello di sinistra si nota inoltre l'avanzo di un perno, di materiale diverso da quello della sfera. Non si hanno notizie sul fatto che sia o no coevo alla sfera.

La faccia anteriore - come si è detto - presenta tre cerchi concentrici. Possiamo anticipare subito che il centro di questi cerchi si trova ad un'altezza sull'orizzonte pari a 44,9 gradi: questo dato va confrontato con la latitudine di Matelica (43,22 gradi). Anche sul significato di questi tre cerchi, e dell'arco che li interseca, torneremo in un momento: per ora completiamo la descrizione notando alcune iscrizioni in greco nel complesso dei cerchi, che sono evidentemente in relazione con le costellazioni dello Zodiaco.

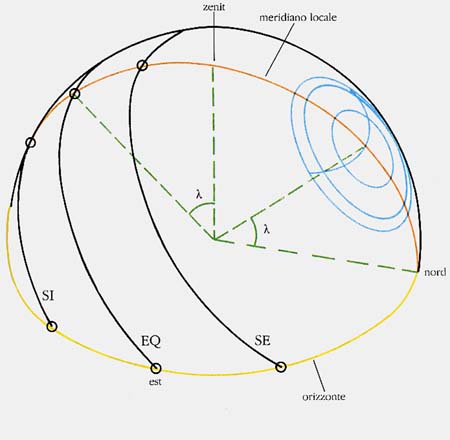
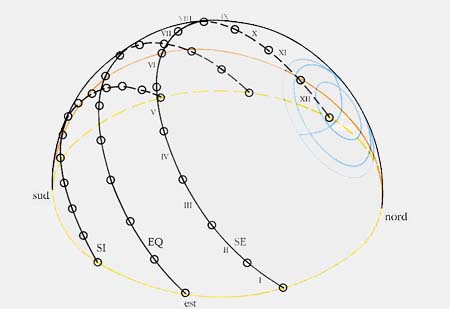
Per comprendere la funzione e il modus operandi dei vari simboli sulla sfera conviene rifarsi al cammino apparente del Sole nel cielo durante l'arco di un anno (figura 1). Alle latitudini intermedie (come quella di Matelica) il Sole sorge esattamente ad est nei giorni dell'equinozio, mentre sorge spostato verso sud o verso nord (di un angolo azimutale che dipende dalla latitudine e dall'inclinazione dell'asse terrestre sul piano orbitale) rispettivamente al solstizio d'inverno e al solstizio d'estate. Tra il solstizio d'inverno (SI) e quello estivo (SE) il punto dell'orizzonte in cui sorge il Sole si sposta gradualmente, passando per l'est; giunto in SE inverte il moto e torna di nuovo verso SI passando ancora per l'est. Nei giorni equinoziali, a mezzogiorno, il Sole transita al meridiano esattamente ad un'altezza sull'orizzonte pari alla colatitudine (90 gradi - latitudine) del posto; a mezzogiorno di SI si troverà ad un'altezza pari alla precedente meno l'obliquità dell'eclittica e, a mezzogiorno di SE, ad un'altezza pari alla precedente più l'obliquità dell'eclittica.

Figura 1 Modello della metà superiore della sfera di Matetica Oltre ali orizzonte (giallo), al meridiano (arancione) e al sistema di cerchi concentrici (azzurro) che è rivolto verso il nord, sono indicate le tre proiezioni del percorso giornaliero del Sole sulla volta celeste nei tre giorni corrispondenti al solstizio d'inverno (SI), agli equinozi (EQ) e al solstizio destate (SE). I cerchietti indicano la posizione del Sole sull'orizzonte (all'alba) e sul meridiano (a mezzogiorno) in questi quattro giorni. L'angolo λ è pari alla latitudine di Matelica.

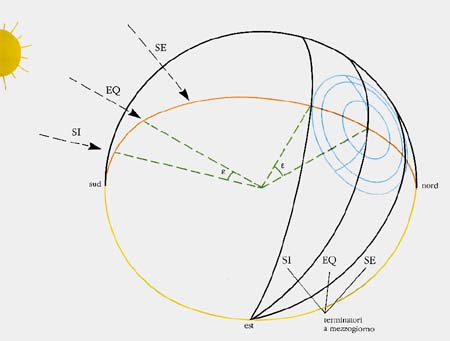
Immaginando di esporre la sfera alla luce del Sole, questi ne illumina la metà, e il limite tra la luce e l'ombra (il terminatore) si trova esattamente a 90 gradi dalla direzione del Sole. Come si vede nella figura 2, se il raggio angolare del cerchio più grande è pari all'obliquità dell' eclittica (ε), il terminatore sarà tangente alla parte superiore del cerchio a mezzodì di SI, passerà per il centro a mezzodì degli equinozi e sarà tangente alla parte inferiore del cerchio a mezzodì di SE. Ora con buona approssimazione (torneremo più oltre su questo argomento), il raggio del cerchio esterno è proprio pari all'obliquità, per cui l'osservazione della posizione del terminatore a mezzogiorno forniva agli utenti della sfera una stima abbastanza precisa della stagione dell'anno.

Figura 2 Posizione dei terminatori a mezzogiorno dei giorni solstiziali (SE, SI) ed equinoziali (EQ). L'angolo ε è pari all'obliquità dell'eclittica (circa 23 gradi).

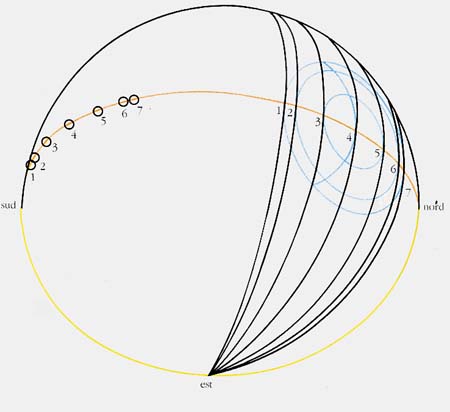
Vi è però molto di più (figura 3): i due cerchi più interni si trovano ad una distanza angolare dal centro tale che il terminatore è ad essi tangente (sempre a mezzogiorno, per semplicità) un mese dopo o un mese prima di SI (parte superiore del secondo cerchio); due mesi dopo o due mesi prima di SI  (parte superiore del terzo cerchio); due mesi prima o due mesi dopo SE (parte inferiore  del terzo cerchio); un mese prima o un mese dopo SE (parte inferiore del secondo cerchio).

Figura 3 Posizione dei terminatori intorno al 20 di ogni mese. Le posizioni del Sole (indicate con dei pallini) e i relativi terminatori sono: 1-solstizio d'inverno; 2-gennaio, novembre; 3-febbraio, ottobre; 4-marzo, settembre (equinozi); 5-aprile, agosto; 6-maggio, luglio; 7-solstizio d'estate.

Utilizzando i nomi e i tempi di oggi potremmo dire che il terminatore è tangente al cerchio esterno a dicembre (in alto) e a giugno (in basso); al secondo cerchio a novembre e gennaio (in alto) e maggio e luglio (in basso); al terzo cerchio a ottobre e febbraio (in alto) e aprile e agosto (in basso); passerà infine per il centro a marzo e settembre. Il sistema di cerchi appare quindi orientato verso il polo nord (assumiamo, per ora, che il centro dei cerchi coincida proprio con la latitudine del posto) e con ampiezza corrispondente alla declinazione che il Sole assume a distanza di un mese tra un solstizio e un equinozio. Si tratta in definitiva di un ottimo calendario, quando la precisione richiesta non sia eccezionale.

La funzione dell'arco di cerchio che passa per il centro è meno evidente: potrebbe semplicemente fornire il rapporto tra la durata del giorno e la durata della notte. Infatti, riportando su ciascun cerchio mensile i due archi in cui viene diviso l'orizzonte dai punti in cui si trova il Sole all'alba e al tramonto, si ottiene una serie di coppie di punti su ciascun cerchio, unendo i quali si ottiene proprio l'arco inciso sul globo (figura 4). Veramente il raggio di questo arco dipenderebbe dalla latitudine e sarebbe un po' più piccolo di quello osservato (di circa 3 mm) se la latitudine del posto fosse proprio quella di Matelica. Come abbiamo visto, però, la latitudine denunciata dal globo è un po' più grande, molto vicina a 45 gradi, valore per il quale il raggio dell'arco di cerchio è - come osservato – pari a quello del cerchio più grande.

Figura 4 L'arco di cerchio (in verde) interseca i tre cerchi concentrici dividendoli in due parti esattamente uguali (come ampiezza angolare) a quelle in cui è diviso l'orizzonte dai punti in cui sorge e tramonta il Sole nei mesi corrispondenti: ad esempio, l'arco 1-1' in viola (passando da sud) sull'orizzonte è uguale all'arco 1-1', nello stesso colore (passando dal basso) sul cerchio esterno.

La discrepanza tra la latitudine del centro dei cerchi e quella di Matelica non è trascurabile. Su una sfera di quasi 15 cm di raggio essa rappresenta un arco di poco più di 4 mm, che ci pare un errore un po' troppo cospicuo, data la precisione con cui lo strumento è stato costruito. Questa differenza, a nostro parere, può essere dovuta a tre possibili cause: 1) gli artefici hanno sbagliato la determinazione della latitudine di Matelica; 2) il globo non era destinato a Matelica, ma ad una città posta all'incirca sul quarantacinquesimo parallelo; 3) gli artefici hanno sbagliato a riportare sul globo la latitudine osservata (che invece era giusta). Abbiamo già detto che quest'ultima ipotesi ci pare improbabile, data l'accurata fattura dell'insieme: un'analisi statistica degli errori di misura di varie lunghezze e archi sulla sfera, infatti, ci rivela che le misure sono consistenti con la latitudine del centro dei cerchi con scarti massimi di 2 mm. La seconda ipotesi richiederebbe un accurato studio sull'origine del globo, sul significato della sua attuale presenza a Matelica, dove sono state rinvenute nel passato suppellettili e monete di origine greca, nonché resti di ville romane, e una giustificazione plausibile dell'eventuale trasporto di uno strumento del genere in una località in cui - per quanto ne sapevano gli utenti - non avrebbe potuto espletare al meglio la sua funzione. Non possiamo discutere ulteriormente questa possibilità, ma possiamo cercare di esaminare meglio la prima.

La determinazione della latitudine di una località comportava, duemila anni fa, la misura della lunghezza dell'ombra proiettata da uno gnomone a mezzogiorno di un giorno equinoziale. Il rapporto tra la lunghezza dell'ombra e la lunghezza dello gnomone è la tangente della latitudine. Non abbiamo mai fatto cenno all'epoca della costruzione della sfera di Matelica ma, stando alla datazione della sfera simile custodita a Nafplion, dovremmo essere nei primi secoli avanti Cristo; a quell'epoca il citato metodo per la determinazione della latitudine era ben noto. Ora, supponendo che lo gnomone di riferimento avesse una lunghezza di circa due metri (vi sono cenni di gnomoni alti come un uomo, usati a questo scopo), una differenza di un grado di latitudine (intorno ai 45 gradi) si traduce in una differenza di circa 7 cm nella lunghezza dell'ombra. Poiché lo scarto tra la latitudine osservata sulla sfera (posizione angolare del centro dei cerchi) e quella vera di Matelica è di 1,68 gradi, questo significa che gli artefici della sfera avrebbero commesso un errore di misura dell'ombra di una dozzina di cm, il che ci pare francamente troppo.

D'altra parte sappiamo che Ipparco scoprì la precessione degli equinozi (cioè la rotazione dell'asse terrestre attorno al polo dell'eclittica in circa 26.000 anni) attorno al secondo secolo avanti Cristo, cioè più o meno all'epoca in cui si presume sia stata costruita la sfera di Nafplion. Possiamo anche supporre che la sfera di Matelica sia antecedente a quella di Nafplion, o - più semplicemente - che le nuove scoperte scientifiche impiegassero all'epoca un certo tempo per tradursi in innovazioni tecnologiche. La precessione degli equinozi fa sì che il giorno - ad esempio - dell'equinozio di primavera si sposti all'indietro di una unità in circa 72 anni. Se l'operazione di misura dell'ombra non viene eseguita esattamente nel giorno dell'equinozio, d'altro canto, si otterrà una misura della latitudine errata (per eccesso o per difetto, a seconda che ci si trovi prima o dopo l'equinozio di primavera, e viceversa all'equinozio d'autunno) di poco meno di mezzo grado al giorno, alla latitudine di Matelica. Se questa ipotesi fosse vera, quindi, potremmo concludere che la misura dell'ombra sia stata fatta circa quattro giorni prima dell'equinozio vero - se in primavera – o quattro giorni dopo se in autunno. In ogni caso si può pensare che la determinazione del giorno equinoziale sia stata in errore di quattro giorni, cioè sia stata fatta circa 300 anni prima della costruzione della sfera. Non conoscendo l'esistenza della precessione degli equinozi, gli artefici di questa non avrebbero avuto nessun motivo di determinare ogni volta quale fosse esattamente il giorno equinoziale.

Naturalmente nulla ci permette di favorire un'ipotesi all'altra, almeno finché non saremo in possesso di una datazione precisa effettuata con metodi archeologici. Per il momento però possiamo assumere che la sfera sia stata costruita per una (presunta?) latitudine di 44,9 gradi.

Abbiamo visto che il sistema di cerchi nella faccia anteriore della sfera permette la determinazione del mese e, con buona volontà, anche della settimana (tanto per indicare una suddivisione più fine del mese). Esso inoltre permette di determinare subito la stagione dell'anno, la distanza temporale da uno dei quattro momenti importanti per l'agricoltura o per eventi civili (i due solstizi e i due equinozi) e fornisce una stima della frazione del giorno in cui c'è luce rispetto a quella al buio.

La sfera, però, è molto più di questo: essa funziona anche come un orologio molto preciso, in grado di fornire l'ora del giorno. Per illustrare come sia possibile determinare l'ora è necessario ricordare che i greci (supponendo che gli utenti della sfera utilizzassero questo sistema) usavano dividere la frazione di giorno tra l'alba e il tramonto in dodici "ore" di uguale lunghezza: in altri termini la loro "ora" non aveva durata costante durante l'anno, ma era più corta d'inverno e più lunga d'estate. Solo attorno agli equinozi la durata dell'"ora" greca (come del resto anche per i romani) equivaleva ad un'ora nostra.

Figura 5 Proiezioni sulla superficie della sfera delle posizioni del Sole all'inizio di ogni "ora" (definita secondo il costume dei greci) nei giorni solstiziali ed equinoziali: i cerchietti corrispondono ai dodicesimi dell'arco diurno descritto dal Sole. Sono indicate le ore nel giorno del solstizio estivo (SE).

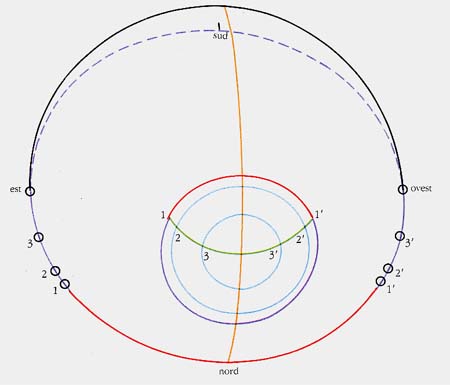
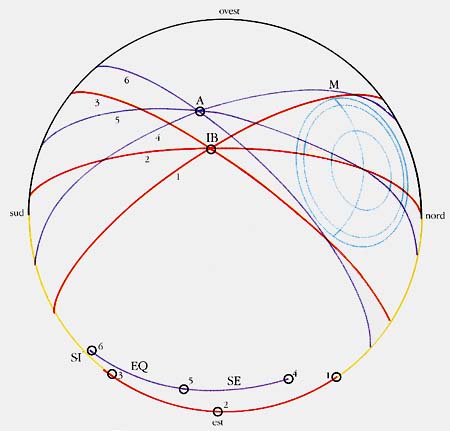
Immaginiamo ora (figura 5) di tracciare il cammino apparente del Sole nel cielo ai due solstizi e all'equinozio: dividendo ciascuno di questi archi in 12 parti otterremo le 12 "ore". Se noi adesso uniamo le posizioni del Sole durante l'anno all'inizio di ogni "ora", otteniamo degli archi di cerchio massimo, che il Sole descrive, una volta in un verso e poi nell'altro, nell'arco di un anno (figura 6). Il primo cerchio (inizio della prima "ora") coincide con l'orizzonte, contenendo tutte le posizioni del Sole all'alba; il sesto cerchio (inizio della sesta "ora") coinciderà invece col meridiano del posto e il cerchio corrispondente ai tramonti (fine della dodicesima "ora") sarà di nuovo l'orizzonte, dall'altra parte dell'alba. Ora, un cerchio su una sfera si dice "massimo" se è ottenuto con l'intersezione di un piano passante per il centro (come nel caso dell'equatore e di tutti i meridiani geografici). Ogni cerchio su una sfera ha un suo "polo", ottenuto dall'intersezione tra la retta passante per il centro, e perpendicolare al piano di sezione, e la superficie della sfera. Solo i cerchi massimi, però, hanno la proprietà di distare, in ogni loro punto, 90 gradi dal polo. È possibile calcolare la posizione dei poli di questi tredici cerchi massimi: essi rappresenteranno gli unici punti della superficie della sfera per i quali, ad una data "ora" durante l'anno, passerà sempre il terminatore, che si trova - come abbiamo detto - a 90 gradi dalla direzione del Sole. Questi poli, intersezione di tutti i terminatori corrispondenti ad una data "ora", coincidono in modo quasi perfetto con le posizioni dei fori sulla faccia posteriore della sfera. È utile notare che la determinazione dei poli, relativamente semplice (ma non banale) con la matematica odierna, non doveva essere un'impresa facile all'epoca della costruzione della sfera: in essa intervenivano sia la latitudine del posto sia il valore dell'obliquità dell'eclittica e richiedeva, naturalmente, che la superficie fosse perfettamente sferica.

Figura 6 In figura sono indicate con dei pallini le posizioni del Sole nella prima ora (1, 2, 3) e nelle seconde ore (4, 5, 6) della giornata; i punti 1 e 4 si riferiscono al solstizio estivo; i punti 3 e 6 al solstizio invernale; i punti 2 e 5 agli equinozi. Collegando come in figura queste posizioni si ottiene il cammino apparente del Sole alla stessa "ora" durante l'anno. Queste curve sono archi di cerchi massimi, i cui poli corrispondono ai fori incisi sulla sfera. Come si vede dalla figura, i terminatori (indicati dai numeri corrispondenti ad una stessa ora durante l'anno), passano comunque per lo stesso foro, che permetteva così di definire l'"ora" del giorno.

Ecco dunque che la sfera si trasforma in un orologio in grado di indicare in quale "ora" ci si trovi. Ricordiamo che per i greci l'"ora" non è un istante, come per noi ad esempio le 8:00, tra le 7:59 e le 8:01, ma tutta la durata di un intervallo temporale pari a un dodicesimo del dì. Guardando tra quali fori cadeva il terminatore, gli utenti erano subito al corrente di quale fosse l'"ora" dell'osservazione. Noi non abbiamo idea delle abitudini di quelle popolazioni, ma la sfera sarebbe in grado di indicare anche frazioni di "ora", fino ad una precisione di circa dieci "minuti".

Correlando la funzione oraria con quella stagionale, osserviamo che, ad esempio al solstizio d'estate, il terminatore all'alba non solo passa per il foro di colmo, che corrisponde allo zenit e indica l'inizio della prima "ora" (ricordiamo che il secondo foro è marcato A: numero uno nella numerazione greca), ma è anche tangente al cerchio più grande (come deve, essendo il solstizio) nel punto di intersezione ("M" in figura 6) con l'arco di cerchio: è l'inizio della giornata. Alla fine della prima "ora" il terminatore passerà per il punto A e sarà ancora tangente al cerchio più grande, ma un po' più avanti, nel punto corrispondente ad un dodicesimo dell'arco di luce (figura 7). Questa situazione si ripresenta ad ogni "ora", cosicché i cerchi mensili possono essere considerati anche come l'inviluppo delle posizioni del terminatore in un determinato giorno dell'anno. 

Figura 7 In uno stesso giorno (quello del solstizio estivo in figura) l'inviluppo dei terminatori (in rosso) nella giornata è il cerchio mensile corrispondente. Notare che il primo terminatore (alba) è tangente al cerchio mensile nel punto in cui questo è intersecato dall'arco di cerchio, mentre l'ultimo terminatore (tramonto) è tangente nell'altro punto d'intersezione. In tal modo era possibile stabilire gli estremi dell'arco di circonferenza che rappresenta  la frazione del giorno illuminata dal  Sole.

Essendo la nostra un'indagine esclusivamente astronomica, non possiamo fare troppe affermazioni di tipo storico-archeologico sui dettagli costruttivi della sfera. Tuttavia possiamo fare qualche accenno ai vincoli che l'osservazione astronomica pone a quelle procedure. Abbiamo già visto che, nell'ipotesi che i costruttori fossero molto abili, forse intervengono problemi sulla determinazione del giorno equinoziale (probabilmente legati all'ignoranza del fenomeno della precessione degli equinozi). Un altro indizio ci viene dalla determinazione del raggio angolare dei cerchi mensili. Per il cerchio più grande esso dovrebbe coincidere con l'obliquità dell'eclittica all'epoca della costruzione. 

Con i metodi di misura angolare da noi adottati (per la verità non estremamente precisi), e tenendo conto delle variazioni secolari di quel parametro, siamo solo in grado di dire che l'obliquità osservata risale ad una data compresa tra il 6000 a.C. e l'epoca attuale; non è un gran risultato!

L'indagine astronomica non può spingersi oltre, ma potrebbe farlo quella archeologica. In che epoca fu costruita la sfera? Forse l'esame del tipo di pietra, dell'avanzo di perno nel foro est, o l'analisi comparata con la sfera di Nafplion potranno dare qualche lume. Per limitarci all'astronomia, cerchiamo di immaginare come si può essere svolta la costruzione di questo strumento. Quanto diremo è altamente speculativo e serve solo come stimolo alla ricerca.  

Innanzitutto, data l'accurata fattura della sfera, non ci pare probabile che si tratti di un caso isolato, come del resto è dimostrato dall'esistenza di almeno un'altra sfera, anche se di concezione diversa. Da qualche parte, nel mondo greco-romano, ci doveva essere una "bottega" che fabbricava sfere. Diamo qui una serie di operazioni possibili per arrivare al risultato che osserviamo oggi.

Prima di tutto gli artigiani fabbricavano un certo numero di sfere perfettamente lisce (e "sferiche") nella parte superiore; incidevano l'"orizzonte" e il "meridiano", più il foro orario di colmo e i due fori (di fissaggio?) sulla base. Avevano probabilmente regoli circolari di legno o bronzo per verificare che il raggio di curvatura fosse costante. Non è escluso che i due fori digamma siano più grandi degli altri proprio per permettere l'alloggiamento di regoli di questo tipo.

Supponiamo ora che alla "bottega" arrivi l'ordinazione di una sfera per una certa città. Gli artefici della sfera avevano solo bisogno di conoscere la latitudine della località di destinazione della sfera, oltre al valore dell'obliquità dell'eclittica. È bene qui notare che, mentre il giorno equinoziale - la cui determinazione precisa permette la misura della latitudine - varia di un'unità ogni 72 anni (per la precessione degli equinozi), l'obliquità varia molto più lentamente (solo 47 secondi d'arco per secolo). E' se non altro ragionevole supporre che la rideterminazione dell'obliquità non fosse uno scrupolo dei costruttori. Forse lo stesso vale anche per la determinazione dell'equinozio: qual era all'epoca il grado di comunicazione tra "scienziati" e "ingegneri"? Noi non lo sappiamo.

Una volta in possesso di questi due parametri, il resto doveva costituire abbastanza una routine. Forse la sfera (imperniata nei fori est ed ovest) era orientata sul meridiano del posto di costruzione e inclinata in modo che la "latitudine" corrispondesse piuttosto a quella del posto di destinazione. In questo modo un'accurata osservazione delle posizioni dei terminatori all'inizio di ogni ora, nell'arco di almeno sei mesi, poteva portare alla definizione delle posizioni dei fori orari e dei cerchi mensili. Non sappiamo se questa è la strada seguita da quegli artigiani, ma senz'altro è una strada percorribile. Altrimenti bisognerebbe supporre alte conoscenze di trigonometria sferica, tali da permettere (con regoli, tabelle, nomogrammi) il posizionamento dei fori orari con grande precisione.

Che funzione hanno i piccoli forellini che si trovano vicino ad alcuni (non tutti) i fori orari? L'unica idea che ci è venuta in mente è che costituissero fori di fissaggio di piccole capsule di bronzo o ferro che aiutassero a determinare l'ora esatta.

Qual era l'uso della sfera? Ovviamente serviva per la misura del tempo, ma da parte di chi? Sulla sfera di Nafplion c'è un'iscrizione in greco che - più o meno - dice "Θαλεια, sacerdote della dea Era, mi ha posto come indicatore quotidiano delle ore solari". Se questa sfera (che non ha simili iscrizioni) ha la medesima origine, forse aveva anche una destinazione simile. A Matelica, allora, si dovrebbero trovare resti di un antico tempio, i cui sacerdoti fossero i custodi dello strumento.

Una prova sperimentale condotta tra il 21 e il 22 di giugno 1988 (data del solstizio d'estate) ha mostrato che i terminatori sono di ben difficile localizzazione (errori superiori a mezzo cm) se la sfera è posta in pieno Sole. Molto meglio sarebbe se, dalla parte opposta al Sole, cioè verso nord, ci fosse un paravento oscuro o - meglio ancora - se la sfera fosse posta in un posto in penombra, con solo un'apertura verso il Sole.

Sono ovviamente illazioni, dovute al buon senso, ma forse i nostri colleghi archeologi potrebbero lavorare su questi elementi per determinare origine, scopi e dettagli costruttivi della sfera.

Sommario	Il cromlech del Piccolo San Bernardo